CF772B.Volatile Kite
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You are given a convex polygon P with n distinct vertices p1,p2,...,pn . Vertex pi has coordinates (xi,yi) in the 2D plane. These vertices are listed in clockwise order.
You can choose a real number D and move each vertex of the polygon a distance of at most D from their original positions.
Find the maximum value of D such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.
输入格式
The first line has one integer n ( 4<=n<=1000 ) — the number of vertices.
The next n lines contain the coordinates of the vertices. Line i contains two integers xi and yi ( −109<=xi,yi<=109 ) — the coordinates of the i -th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon (in particular, no three consecutive points lie on the same straight line).
输出格式
Print one real number D , which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.
Your answer will be considered correct if its absolute or relative error does not exceed 10−6 .
Namely, let's assume that your answer is a and the answer of the jury is b . The checker program will consider your answer correct if 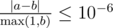 .
.
输入输出样例
输入#1
4 0 0 0 1 1 1 1 0
输出#1
0.3535533906
输入#2
6 5 0 10 0 12 -4 10 -8 5 -8 3 -4
输出#2
1.0000000000
说明/提示
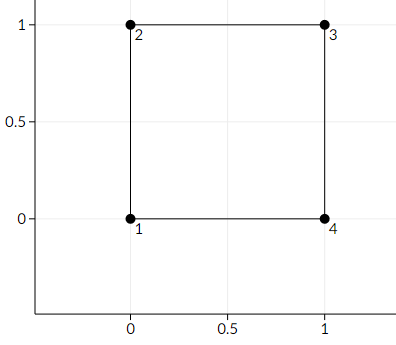
Here is a picture of the first sample
Here is an example of making the polygon non-convex.
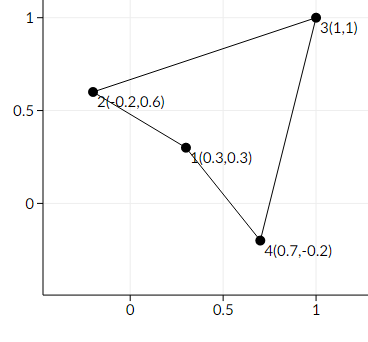
This is not an optimal solution, since the maximum distance we moved one point is ≈0.4242640687 , whereas we can make it non-convex by only moving each point a distance of at most ≈0.3535533906 .