CF772D.Varying Kibibits

You are given $n$ integers $a_{1},a_{2},...,a_{n}$ . Denote this list of integers as $T$ .

Let $f(L)$ be a function that takes in a non-empty list of integers $L$ .

The function will output another integer as follows:

• First, all integers in $L$ are padded with leading zeros so they are all the same length as the maximum length number in $L$ .
• We will construct a string where the $i$ -th character is the minimum of the $i$ -th character in padded input numbers.
• The output is the number representing the string interpreted in base 10.

For example $f(10,9)=0$ , $f(123,321)=121$ , $f(530,932,81)=30$ .

Define the function

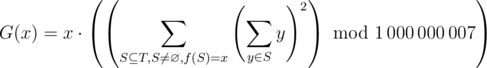Here, denotes a subsequence.In other words, $G(x)$ is the sum of squares of sum of elements of nonempty subsequences of $T$ that evaluate to $x$ when plugged into $f$ modulo $1000000007$ , then multiplied by $x$ . The last multiplication is not modded.

You would like to compute $G(0),G(1),...,G(999999)$ . To reduce the output size, print the value 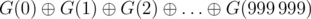, where denotes the bitwise XOR operator.

The first line contains the integer $n$ ( $1<=n<=1000000$ ) — the size of list $T$ .

The next line contains $n$ space-separated integers, $a_{1},a_{2},...,a_{n}$ ( $0<=a_{i}<=999999$ ) — the elements of the list.

Output a single integer, the answer to the problem.

For the first sample, the nonzero values of $G$ are $G(121)=144611577$ , $G(123)=58401999$ , $G(321)=279403857$ , $G(555)=170953875$ . The bitwise XOR of these numbers is equal to $292711924$ .

For example, 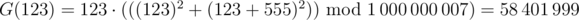, since the subsequences $[123]$ and $[123,555]$ evaluate to $123$ when plugged into $f$ .

For the second sample, we have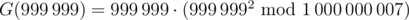

For the last sample, we have 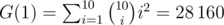, where 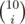is the binomial coefficient.