CF780C.Andryusha and Colored Balloons

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Andryusha goes through a park each day. The squares and paths between them look boring to Andryusha, so he decided to decorate them.

The park consists of $n$ squares connected with $(n-1)$ bidirectional paths in such a way that any square is reachable from any other using these paths. Andryusha decided to hang a colored balloon at each of the squares. The baloons' colors are described by positive integers, starting from $1$ . In order to make the park varicolored, Andryusha wants to choose the colors in a special way. More precisely, he wants to use such colors that if $a$ , $b$ and $c$ are distinct squares that $a$ and $b$ have a direct path between them, and $b$ and $c$ have a direct path between them, then balloon colors on these three squares are distinct.

Andryusha wants to use as little different colors as possible. Help him to choose the colors!

输入格式

The first line contains single integer $n$ ( $3<=n<=2·10^{5}$ ) — the number of squares in the park.

Each of the next $(n-1)$ lines contains two integers $x$ and $y$ ( $1<=x,y<=n$ ) — the indices of two squares directly connected by a path.

It is guaranteed that any square is reachable from any other using the paths.

输出格式

In the first line print single integer $k$ — the minimum number of colors Andryusha has to use.

In the second line print $n$ integers, the $i$ -th of them should be equal to the balloon color on the $i$ -th square. Each of these numbers should be within range from $1$ to $k$ .

输入输出样例

输入#1
```
3
2 3
1 3
```
输出#1
```
3
1 3 2 
```
输入#2
```
5
2 3
5 3
4 3
1 3
```
输出#2
```
5
1 3 2 5 4 
```
输入#3
```
5
2 1
3 2
4 3
5 4
```
输出#3
```
3
1 2 3 1 2 
```

说明/提示

In the first sample the park consists of three squares: $1→3→2$ . Thus, the balloon colors have to be distinct.

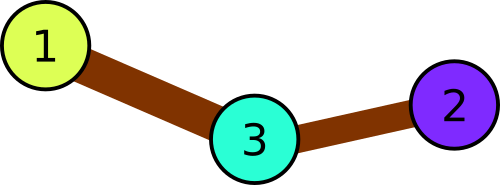Illustration for the first sample.In the second example there are following triples of consequently connected squares:

$1→3→2$
$1→3→4$
$1→3→5$
$2→3→4$
$2→3→5$
$4→3→5$

We can see that each pair of squares is encountered in some triple, so all colors have to be distinct. 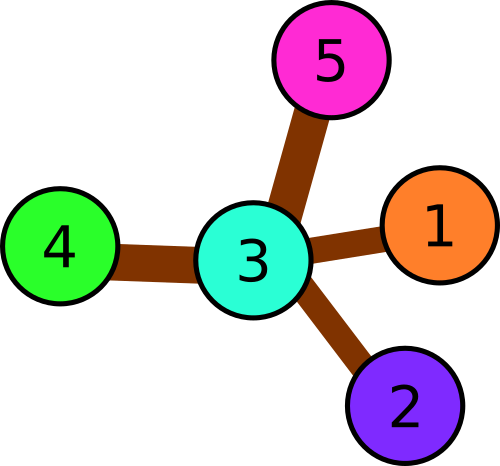Illustration for the second sample.In the third example there are following triples:

$1→2→3$
$2→3→4$
$3→4→5$

We can see that one or two colors is not enough, but there is an answer that uses three colors only. 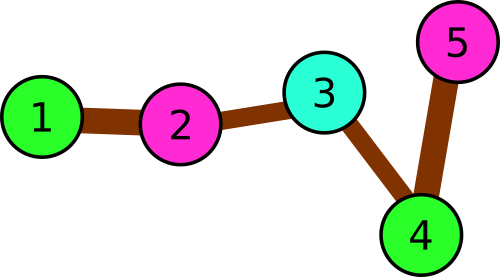Illustration for the third sample.

首页