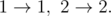CF757C.Felicity is Coming!

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

It's that time of the year, Felicity is around the corner and you can see people celebrating all around the Himalayan region. The Himalayan region has $n$ gyms. The $i$ -th gym has $g_{i}$ Pokemon in it. There are $m$ distinct Pokemon types in the Himalayan region numbered from $1$ to $m$ . There is a special evolution camp set up in the fest which claims to evolve any Pokemon. The type of a Pokemon could change after evolving, subject to the constraint that if two Pokemon have the same type before evolving, they will have the same type after evolving. Also, if two Pokemon have different types before evolving, they will have different types after evolving. It is also possible that a Pokemon has the same type before and after evolving.

Formally, an evolution plan is a permutation $f$ of ${1,2,...,m}$ , such that $f(x)=y$ means that a Pokemon of type $x$ evolves into a Pokemon of type $y$ .

The gym leaders are intrigued by the special evolution camp and all of them plan to evolve their Pokemons. The protocol of the mountain states that in each gym, for every type of Pokemon, the number of Pokemon of that type before evolving any Pokemon should be equal the number of Pokemon of that type after evolving all the Pokemons according to the evolution plan. They now want to find out how many distinct evolution plans exist which satisfy the protocol.

Two evolution plans $f_{1}$ and $f_{2}$ are distinct, if they have at least one Pokemon type evolving into a different Pokemon type in the two plans, i. e. there exists an $i$ such that $f_{1}(i)≠f_{2}(i)$ .

Your task is to find how many distinct evolution plans are possible such that if all Pokemon in all the gyms are evolved, the number of Pokemon of each type in each of the gyms remains the same. As the answer can be large, output it modulo $10^{9}+7$ .

输入格式

The first line contains two integers $n$ and $m$ ( $1<=n<=10^{5}$ , $1<=m<=10^{6}$ ) — the number of gyms and the number of Pokemon types.

The next $n$ lines contain the description of Pokemons in the gyms. The $i$ -th of these lines begins with the integer $g_{i}$ ( $1<=g_{i}<=10^{5}$ ) — the number of Pokemon in the $i$ -th gym. After that $g_{i}$ integers follow, denoting types of the Pokemons in the $i$ -th gym. Each of these integers is between $1$ and $m$ .

The total number of Pokemons (the sum of all $g_{i}$ ) does not exceed $5·10^{5}$ .

输出格式

Output the number of valid evolution plans modulo $10^{9}+7$ .

输入输出样例

输入#1
```
2 3
2 1 2
2 2 3
```
输出#1
```
1
```
输入#2
```
1 3
3 1 2 3
```
输出#2
```
6
```
输入#3
```
2 4
2 1 2
3 2 3 4
```
输出#3
```
2
```
输入#4
```
2 2
3 2 2 1
2 1 2
```
输出#4
```
1
```
输入#5
```
3 7
2 1 2
2 3 4
3 5 6 7
```
输出#5
```
24
```

说明/提示

In the first case, the only possible evolution plan is:

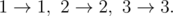In the second case, any permutation of $(1,2,3)$ is valid.

In the third case, there are two possible plans:

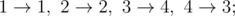
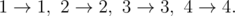In the fourth case, the only possible evolution plan is:

首页