CF715C.Digit Tree

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

ZS the Coder has a large tree. It can be represented as an undirected connected graph of $n$ vertices numbered from $0$ to $n-1$ and $n-1$ edges between them. There is a single nonzero digit written on each edge.

One day, ZS the Coder was bored and decided to investigate some properties of the tree. He chose a positive integer $M$ , which is coprime to $10$ , i.e. .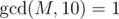

ZS consider an ordered pair of distinct vertices $(u,v)$ interesting when if he would follow the shortest path from vertex $u$ to vertex $v$ and write down all the digits he encounters on his path in the same order, he will get a decimal representaion of an integer divisible by $M$ .

Formally, ZS consider an ordered pair of distinct vertices $(u,v)$ interesting if the following states true:

Let $a_{1}=u,a_{2},...,a_{k}=v$ be the sequence of vertices on the shortest path from $u$ to $v$ in the order of encountering them;
Let $d_{i}$ ( 1<=i<k ) be the digit written on the edge between vertices $a_{i}$ and $a_{i+1}$ ;
The integer 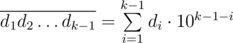is divisible by $M$ .

Help ZS the Coder find the number of interesting pairs!

输入格式

The first line of the input contains two integers, $n$ and $M$ ( $2<=n<=100000$ , $1<=M<=10^{9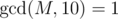}$ , ) — the number of vertices and the number ZS has chosen respectively.

The next $n-1$ lines contain three integers each. $i$ -th of them contains $u_{i},v_{i}$ and $w_{i}$ , denoting an edge between vertices $u_{i}$ and $v_{i}$ with digit $w_{i}$ written on it ( 0<=u_{i},v_{i}<n,1<=w_{i}<=9 ).

输出格式

Print a single integer — the number of interesting (by ZS the Coder's consideration) pairs.

输入输出样例

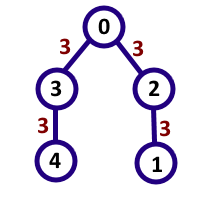
输入#1
```
6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7
```
输出#1
```
7
```
输入#2
```
5 11
1 2 3
2 0 3
3 0 3
4 3 3
```
输出#2
```
8
```

说明/提示

In the first sample case, the interesting pairs are $(0,4),(1,2),(1,5),(3,2),(2,5),(5,2),(3,5)$ . The numbers that are formed by these pairs are $14,21,217,91,7,7,917$ respectively, which are all multiples of $7$ . Note that $(2,5)$ and $(5,2)$ are considered different.

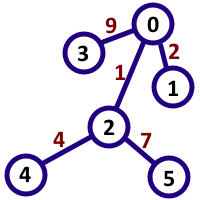In the second sample case, the interesting pairs are $(4,0),(0,4),(3,2),(2,3),(0,1),(1,0),(4,1),(1,4)$ , and $6$ of these pairs give the number $33$ while $2$ of them give the number $3333$ , which are all multiples of $11$ .

首页