CF715E.Complete the Permutations

ZS the Coder is given two permutations $p$ and $q$ of ${1,2,...,n}$ , but some of their elements are replaced with $0$ . The distance between two permutations $p$ and $q$ is defined as the minimum number of moves required to turn $p$ into $q$ . A move consists of swapping exactly $2$ elements of $p$ .

ZS the Coder wants to determine the number of ways to replace the zeros with positive integers from the set ${1,2,...,n}$ such that $p$ and $q$ are permutations of ${1,2,...,n}$ and the distance between $p$ and $q$ is exactly $k$ .

ZS the Coder wants to find the answer for all $0<=k<=n-1$ . Can you help him?

The first line of the input contains a single integer $n$ ( $1<=n<=250$ ) — the number of elements in the permutations.

The second line contains $n$ integers, $p_{1},p_{2},...,p_{n}$ ( $0<=p_{i}<=n$ ) — the permutation $p$ . It is guaranteed that there is at least one way to replace zeros such that $p$ is a permutation of ${1,2,...,n}$ .

The third line contains $n$ integers, $q_{1},q_{2},...,q_{n}$ ( $0<=q_{i}<=n$ ) — the permutation $q$ . It is guaranteed that there is at least one way to replace zeros such that $q$ is a permutation of ${1,2,...,n}$ .

Print $n$ integers, $i$ -th of them should denote the answer for $k=i-1$ . Since the answer may be quite large, and ZS the Coder loves weird primes, print them modulo $998244353=2^{23}·7·17+1$ , which is a prime.

In the first sample case, there is the only way to replace zeros so that it takes $0$ swaps to convert $p$ into $q$ , namely $p=(1,2,3),q=(1,2,3)$ .

There are two ways to replace zeros so that it takes $1$ swap to turn $p$ into $q$ . One of these ways is $p=(1,2,3),q=(3,2,1)$ , then swapping $1$ and $3$ from $p$ transform it into $q$ . The other way is $p=(1,3,2),q=(1,2,3)$ . Swapping $2$ and $3$ works in this case.

Finally, there is one way to replace zeros so that it takes $2$ swaps to turn $p$ into $q$ , namely $p=(1,3,2),q=(3,2,1)$ . Then, we can transform $p$ into $q$ like following: 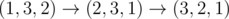.