CF717I.Cowboy Beblop at his computer
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Cowboy Beblop is a funny little boy who likes sitting at his computer. He somehow obtained two elastic hoops in the shape of 2D polygons, which are not necessarily convex. Since there's no gravity on his spaceship, the hoops are standing still in the air. Since the hoops are very elastic, Cowboy Beblop can stretch, rotate, translate or shorten their edges as much as he wants.
For both hoops, you are given the number of their vertices, as well as the position of each vertex, defined by the X , Y and Z coordinates. The vertices are given in the order they're connected: the 1st vertex is connected to the 2nd, which is connected to the 3rd, etc., and the last vertex is connected to the first one. Two hoops are connected if it's impossible to pull them to infinity in different directions by manipulating their edges, without having their edges or vertices intersect at any point – just like when two links of a chain are connected. The polygons' edges do not intersect or overlap.
To make things easier, we say that two polygons are well-connected, if the edges of one polygon cross the area of the other polygon in two different directions (from the upper and lower sides of the plane defined by that polygon) a different number of times.
Cowboy Beblop is fascinated with the hoops he has obtained and he would like to know whether they are well-connected or not. Since he’s busy playing with his dog, Zwei, he’d like you to figure it out for him. He promised you some sweets if you help him!
输入格式
The first line of input contains an integer n ( 3<=n<=100000 ), which denotes the number of edges of the first polygon. The next N lines each contain the integers x , y and z ( −1000000<=x,y,z<=1000000 ) — coordinates of the vertices, in the manner mentioned above. The next line contains an integer m ( 3<=m<=100000 ) , denoting the number of edges of the second polygon, followed by m lines containing the coordinates of the second polygon’s vertices.
It is guaranteed that both polygons are simple (no self-intersections), and in general that the obtained polygonal lines do not intersect each other. Also, you can assume that no 3 consecutive points of a polygon lie on the same line.
输出格式
Your output should contain only one line, with the words "YES" or "NO", depending on whether the two given polygons are well-connected.
输入输出样例
输入#1
4 0 0 0 2 0 0 2 2 0 0 2 0 4 1 1 -1 1 1 1 1 3 1 1 3 -1
输出#1
YES
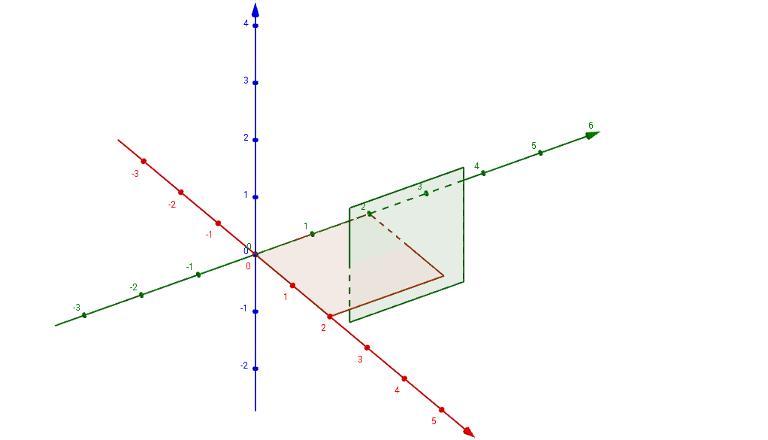
说明/提示
On the picture below, the two polygons are well-connected, as the edges of the vertical polygon cross the area of the horizontal one exactly once in one direction (for example, from above to below), and zero times in the other (in this case, from below to above). Note that the polygons do not have to be parallel to any of the xy-,xz-,yz- planes in general.