CF698F.Coprime Permutation

Two positive integers are coprime if and only if they don't have a common divisor greater than $1$ .

Some bear doesn't want to tell Radewoosh how to solve some algorithmic problem. So, Radewoosh is going to break into that bear's safe with solutions. To pass through the door, he must enter a permutation of numbers $1$ through $n$ . The door opens if and only if an entered permutation $p_{1},p_{2},...,p_{n}$ satisfies:

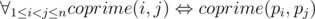In other words, two different elements are coprime if and only if their indices are coprime.

Some elements of a permutation may be already fixed. In how many ways can Radewoosh fill the remaining gaps so that the door will open? Print the answer modulo $10^{9}+7$ .

The first line of the input contains one integer $n$ ( $2<=n<=1000000$ ).

The second line contains $n$ integers $p_{1},p_{2},...,p_{n}$ ( $0<=p_{i}<=n$ ) where $p_{i}=0$ means a gap to fill, and $p_{i}>=1$ means a fixed number.

It's guaranteed that if $i≠j$ and $p_{i},p_{j}>=1$ then $p_{i}≠p_{j}$ .

Print the number of ways to fill the gaps modulo $10^{9}+7$ (i.e. modulo $1000000007$ ).

In the first sample test, none of four element is fixed. There are four permutations satisfying the given conditions: (1,2,3,4), (1,4,3,2), (3,2,1,4), (3,4,1,2).

In the second sample test, there must be $p_{3}=1$ and $p_{4}=2$ . The two permutations satisfying the conditions are: (3,4,1,2,5), (5,4,1,2,3).