CF708D.Incorrect Flow
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
At the entrance examination for the magistracy of the MSU Cyber-Mechanics Department Sasha got the question about Ford-Fulkerson algorithm. He knew the topic perfectly as he worked with it many times on programming competition. As the task for the question he was given a network with partially build flow that he had to use in order to demonstrate the workflow of the algorithm. He quickly finished to write the text and took a look at the problem only to understand that the given network is incorrect!
Suppose you are given a directed graph G(V,E) with two special nodes s and t called source and sink. We denote as n the number of nodes in the graph, i.e. n=∣V∣ and m stands for the number of directed edges in the graph, i.e. m=∣E∣ . For the purpose of this problem we always consider node 1 to be the source and node n to be the sink. In addition, for each edge of the graph e we define the capacity function c(e) and flow function f(e) . Function f(e) represents the correct flow if the following conditions are satisfied:
- For each edge
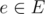 the flow is non-negative and does not exceed capacity c(e) , i.e. 0<=f(e)<=c(e) .
the flow is non-negative and does not exceed capacity c(e) , i.e. 0<=f(e)<=c(e) . - For each node
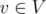 , that is not source or sink ( v=s and v=t ) the sum of flows of all edges going in v is equal to the sum of the flows among all edges going out from v . In other words, there is no flow stuck in v .
, that is not source or sink ( v=s and v=t ) the sum of flows of all edges going in v is equal to the sum of the flows among all edges going out from v . In other words, there is no flow stuck in v .
It was clear that as the exam was prepared last night and there are plenty of mistakes in the tasks. Sasha asked one of the professors to fix the network or give the correct task, but the reply was that the magistrate student should be able to fix the network himself. As the professor doesn't want the task to become easier, he asks Sasha to fix the network in a such way that the total number of changes is minimum possible. Sasha is not allowed to remove edges, add new ones or reverse the direction of existing edges. The only thing he is able to do is to change capacity function c(e) and flow function f(e) . Moreover, all the values should remain non-negative integers. There is no requirement on the flow to be maximum in any sense.
Find the minimum possible total change of the functions f(e) and c(e) that Sasha has to make in order to make the flow correct. The total change is defined as the sum of absolute differences, i.e. if new functions are f∗(e) and c∗(e) , then the total change is 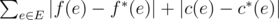 .
.
输入格式
The first line of the input contains two integers n and m ( 2<=n<=100 , 0<=m<=100 ) — the number of nodes and edges in the graph respectively. Each of the following m lines contains the description of the edges, consisting of four integers ui , vi , ci and fi ( 1<=ui,vi<=n , ui=vi , 0<=ci,fi<=1000000 ) — index of the node the edges starts from, the index of the node the edge goes to, current capacity and flow value.
Node number 1 is the source, and node number n is the sink. It's guaranteed that no edge goes to the source, and no edges starts in the sink.
Given graph contains no self-loops but may contain multiple edges.
输出格式
Print one integer — the minimum total sum of changes that Sasha has to do in order to get the correct flow description.
输入输出样例
输入#1
2 1 1 2 2 1
输出#1
0
输入#2
2 1 1 2 1 2
输出#2
1
输入#3
3 3 1 2 1 1 2 3 2 2 1 3 3 3
输出#3
1
输入#4
4 2 2 3 1 1 3 2 1 1
输出#4
0
说明/提示
In the first sample, the flow is initially correct. Note, that the flow is not maximum, but this is not required.
In the second sample, the flow value of the only edge is greater than its capacity. There are two ways to fix this: either increase the capacity up to 2 or reduce the flow down to 1 .
In the third sample, there is only 1 unit of flow coming to vertex 2 , but there are 2 units going out of it. One of the possible solutions is to reduce the value of the flow on the second edge by 1 .
In the fourth sample, there is isolated circulation of flow, but this description is correct by definition.