CF679D.Bear and Chase

Bearland has $n$ cities, numbered $1$ through $n$ . There are $m$ bidirectional roads. The $i$ -th road connects two distinct cities $a_{i}$ and $b_{i}$ . No two roads connect the same pair of cities. It's possible to get from any city to any other city (using one or more roads).

The distance between cities $a$ and $b$ is defined as the minimum number of roads used to travel between $a$ and $b$ .

Limak is a grizzly bear. He is a criminal and your task is to catch him, or at least to try to catch him. You have only two days (today and tomorrow) and after that Limak is going to hide forever.

Your main weapon is BCD (Bear Criminal Detector). Where you are in some city, you can use BCD and it tells you the distance between you and a city where Limak currently is. Unfortunately, BCD can be used only once a day.

You don't know much about Limak's current location. You assume that he is in one of $n$ cities, chosen uniformly at random (each city with probability ). You decided for the following plan:

1. Choose one city and use BCD there.

• After using BCD you can try to catch Limak (but maybe it isn't a good idea). In this case you choose one city and check it. You win if Limak is there. Otherwise, Limak becomes more careful and you will never catch him (you loose).

2. Wait $24$ hours to use BCD again. You know that Limak will change his location during that time. In detail, he will choose uniformly at random one of roads from his initial city, and he will use the chosen road, going to some other city.
3. Tomorrow, you will again choose one city and use BCD there.
4. Finally, you will try to catch Limak. You will choose one city and check it. You will win if Limak is there, and loose otherwise.

Each time when you choose one of cities, you can choose any of $n$ cities. Let's say it isn't a problem for you to quickly get somewhere.

What is the probability of finding Limak, if you behave optimally?

The first line of the input contains two integers $n$ and $m$ ( $2<=n<=400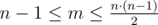$ , ) — the number of cities and the number of roads, respectively.

Then, $m$ lines follow. The $i$ -th of them contains two integers $a_{i}$ and $b_{i}$ ( $1<=a_{i},b_{i}<=n$ , $a_{i}≠b_{i}$ ) — cities connected by the $i$ -th road.

No two roads connect the same pair of cities. It's possible to get from any city to any other city.

Print one real number — the probability of finding Limak, if you behave optimally. Your answer will be considered correct if its absolute error does not exceed $10^{-6}$ .

Namely: let's assume that your answer is $a$ , and the answer of the jury is $b$ . The checker program will consider your answer correct if $|a-b|<=10^{-6}$ .

In the first sample test, there are three cities and there is a road between every pair of cities. Let's analyze one of optimal scenarios.

1. Use BCD in city $1$ .

• With probability Limak is in this city and BCD tells you that the distance is $0$ . You should try to catch him now and you win for sure.
• With probability the distance is $1$ because Limak is in city $2$ or city $3$ . In this case you should wait for the second day.

2. You wait and Limak moves to some other city.

• There is probability 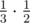that Limak was in city $2$ and then went to city $3$ .
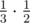• that he went from $2$ to $1$ .
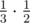• that he went from $3$ to $2$ .
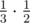• that he went from $3$ to $1$ .

3. Use BCD again in city $1$ (though it's allowed to use it in some other city).

• If the distance is $0$ then you're sure Limak is in this city (you win).
• If the distance is $1$ then Limak is in city $2$ or city $3$ . Then you should guess that he is in city $2$ (guessing city $3$ would be fine too).

You loose only if Limak was in city $2$ first and then he moved to city $3$ . The probability of loosing is 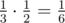. The answer is .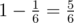