CF689B.Mike and Shortcuts
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Recently, Mike was very busy with studying for exams and contests. Now he is going to chill a bit by doing some sight seeing in the city.
City consists of n intersections numbered from 1 to n . Mike starts walking from his house located at the intersection number 1 and goes along some sequence of intersections. Walking from intersection number i to intersection j requires ∣i−j∣ units of energy. The total energy spent by Mike to visit a sequence of intersections p1=1,p2,...,pk is equal to 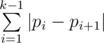 units of energy.
units of energy.
Of course, walking would be boring if there were no shortcuts. A shortcut is a special path that allows Mike walking from one intersection to another requiring only 1 unit of energy. There are exactly n shortcuts in Mike's city, the ith of them allows walking from intersection i to intersection ai ( i<=ai<=ai+1 ) (but not in the opposite direction), thus there is exactly one shortcut starting at each intersection. Formally, if Mike chooses a sequence p1=1,p2,...,pk then for each 1<=i<k satisfying pi+1=api and api=pi Mike will spend only 1 unit of energy instead of ∣pi−pi+1∣ walking from the intersection pi to intersection pi+1 . For example, if Mike chooses a sequence p1=1,p2=ap1,p3=ap2,...,pk=apk−1 , he spends exactly k−1 units of total energy walking around them.
Before going on his adventure, Mike asks you to find the minimum amount of energy required to reach each of the intersections from his home. Formally, for each 1<=i<=n Mike is interested in finding minimum possible total energy of some sequence p1=1,p2,...,pk=i .
输入格式
The first line contains an integer n (1<=n<=200000) — the number of Mike's city intersection.
The second line contains n integers a1,a2,...,an (i<=ai<=n , 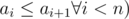 , describing shortcuts of Mike's city, allowing to walk from intersection i to intersection ai using only 1 unit of energy. Please note that the shortcuts don't allow walking in opposite directions (from ai to i ).
, describing shortcuts of Mike's city, allowing to walk from intersection i to intersection ai using only 1 unit of energy. Please note that the shortcuts don't allow walking in opposite directions (from ai to i ).
输出格式
In the only line print n integers m1,m2,...,mn , where mi denotes the least amount of total energy required to walk from intersection 1 to intersection i .
输入输出样例
输入#1
3 2 2 3
输出#1
0 1 2
输入#2
5 1 2 3 4 5
输出#2
0 1 2 3 4
输入#3
7 4 4 4 4 7 7 7
输出#3
0 1 2 1 2 3 3
说明/提示
In the first sample case desired sequences are:
1:1 ; m1=0 ;
2:1,2 ; m2=1 ;
3:1,3 ; m3=∣3−1∣=2 .
In the second sample case the sequence for any intersection 1<i is always 1,i and mi=∣1−i∣ .
In the third sample case — consider the following intersection sequences:
1:1 ; m1=0 ;
2:1,2 ; m2=∣2−1∣=1 ;
3:1,4,3 ; m3=1+∣4−3∣=2 ;
4:1,4 ; m4=1 ;
5:1,4,5 ; m5=1+∣4−5∣=2 ;
6:1,4,6 ; m6=1+∣4−6∣=3 ;
7:1,4,5,7 ; m7=1+∣4−5∣+1=3 .