CF633E.Startup Funding
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
An e-commerce startup pitches to the investors to get funding. They have been functional for n weeks now and also have a website!
For each week they know the number of unique visitors during this week vi and the revenue ci . To evaluate the potential of the startup at some range of weeks from l to r inclusive investors use the minimum among the maximum number of visitors multiplied by 100 and the minimum revenue during this period, that is:
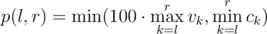 The truth is that investors have no idea how to efficiently evaluate the startup, so they are going to pick some k random distinct weeks li and give them to managers of the startup. For each li they should pick some ri>=li and report maximum number of visitors and minimum revenue during this period.
The truth is that investors have no idea how to efficiently evaluate the startup, so they are going to pick some k random distinct weeks li and give them to managers of the startup. For each li they should pick some ri>=li and report maximum number of visitors and minimum revenue during this period.
Then, investors will calculate the potential of the startup for each of these ranges and take minimum value of p(li,ri) as the total evaluation grade of the startup. Assuming that managers of the startup always report the optimal values of ri for some particular li , i.e., the value such that the resulting grade of the startup is maximized, what is the expected resulting grade of the startup?
输入格式
The first line of the input contains two integers n and k ( 1<=k<=n<=1000000 ).
The second line contains n integers vi ( 1<=vi<=107 ) — the number of unique visitors during each week.
The third line contains n integers ci ( 1<=ci<=107 ) —the revenue for each week.
输出格式
Print a single real value — the expected grade of the startup. Your answer will be considered correct if its absolute or relative error does not exceed 10−6 .
Namely: let's assume that your answer is a , and the answer of the jury is b . The checker program will consider your answer correct, if 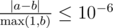 .
.
输入输出样例
输入#1
3 2 3 2 1 300 200 300
输出#1
133.3333333
说明/提示
Consider the first sample.
If the investors ask for li=1 onwards, startup will choose ri=1 , such that max number of visitors is 3 and minimum revenue is 300 . Thus, potential in this case is min(3⋅100,300)=300 .
If the investors ask for li=2 onwards, startup will choose ri=3 , such that max number of visitors is 2 and minimum revenue is 200 . Thus, potential in this case is min(2⋅100,200)=200 .
If the investors ask for li=3 onwards, startup will choose ri=3 , such that max number of visitors is 1 and minimum revenue is 300 . Thus, potential in this case is min(1⋅100,300)=100 .
We have to choose a set of size 2 equi-probably and take minimum of each. The possible sets here are : 200,300 , 100,300 , 100,200 , effectively the set of possible values as perceived by investors equi-probably: 200,100,100 . Thus, the expected value is (100+200+100)/3=133.(3) .