CF639C.Bear and Polynomials

Limak is a little polar bear. He doesn't have many toys and thus he often plays with polynomials.

He considers a polynomial valid if its degree is $n$ and its coefficients are integers not exceeding $k$ by the absolute value. More formally:

Let $a_{0},a_{1},...,a_{n}$ denote the coefficients, so 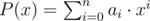. Then, a polynomial $P(x)$ is valid if all the following conditions are satisfied:

• $a_{i}$ is integer for every $i$ ;
• $|a_{i}|<=k$ for every $i$ ;
• $a_{n}≠0$ .

Limak has recently got a valid polynomial $P$ with coefficients $a_{0},a_{1},a_{2},...,a_{n}$ . He noticed that $P(2)≠0$ and he wants to change it. He is going to change one coefficient to get a valid polynomial $Q$ of degree $n$ that $Q(2)=0$ . Count the number of ways to do so. You should count two ways as a distinct if coefficients of target polynoms differ.

The first line contains two integers $n$ and $k$ ( $1<=n<=200000,1<=k<=10^{9}$ ) — the degree of the polynomial and the limit for absolute values of coefficients.

The second line contains $n+1$ integers $a_{0},a_{1},...,a_{n}$ ( $|a_{i}|<=k,a_{n}≠0$ ) — describing a valid polynomial 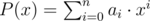. It's guaranteed that $P(2)≠0$ .

Print the number of ways to change one coefficient to get a valid polynomial $Q$ that $Q(2)=0$ .

In the first sample, we are given a polynomial $P(x)=10-9x-3x^{2}+5x^{3}$ .

Limak can change one coefficient in three ways:

1. He can set $a_{0}=-10$ . Then he would get $Q(x)=-10-9x-3x^{2}+5x^{3}$ and indeed $Q(2)=-10-18-12+40=0$ .
2. Or he can set $a_{2}=-8$ . Then $Q(x)=10-9x-8x^{2}+5x^{3}$ and indeed $Q(2)=10-18-32+40=0$ .
3. Or he can set $a_{1}=-19$ . Then $Q(x)=10-19x-3x^{2}+5x^{3}$ and indeed $Q(2)=10-38-12+40=0$ .

In the second sample, we are given the same polynomial. This time though, $k$ is equal to $12$ instead of $10^{9}$ . Two first of ways listed above are still valid but in the third way we would get |a_{1}|>k what is not allowed. Thus, the answer is $2$ this time.