CF639E.Bear and Paradox
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Limak is a big polar bear. He prepared n problems for an algorithmic contest. The i -th problem has initial score pi . Also, testers said that it takes ti minutes to solve the i -th problem. Problems aren't necessarily sorted by difficulty and maybe harder problems have smaller initial score but it's too late to change it — Limak has already announced initial scores for problems. Though it's still possible to adjust the speed of losing points, denoted by c in this statement.
Let T denote the total number of minutes needed to solve all problems (so, T=t1+t2+...+tn ). The contest will last exactly T minutes. So it's just enough to solve all problems.
Points given for solving a problem decrease linearly. Solving the i -th problem after x minutes gives exactly 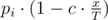 points, where
points, where 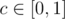 is some real constant that Limak must choose.
is some real constant that Limak must choose.
Let's assume that c is fixed. During a contest a participant chooses some order in which he or she solves problems. There are n! possible orders and each of them gives some total number of points, not necessarily integer. We say that an order is optimal if it gives the maximum number of points. In other words, the total number of points given by this order is greater or equal than the number of points given by any other order. It's obvious that there is at least one optimal order. However, there may be more than one optimal order.
Limak assumes that every participant will properly estimate ti at the very beginning and will choose some optimal order. He also assumes that testers correctly predicted time needed to solve each problem.
For two distinct problems i and j such that p_{i}<p_{j} Limak wouldn't be happy to see a participant with strictly more points for problem i than for problem j . He calls such a situation a paradox.
It's not hard to prove that there will be no paradox for c=0 . The situation may be worse for bigger c . What is the maximum real value c (remember that 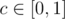 ) for which there is no paradox possible, that is, there will be no paradox for any optimal order of solving problems?
) for which there is no paradox possible, that is, there will be no paradox for any optimal order of solving problems?
It can be proved that the answer (the maximum c as described) always exists.
输入格式
The first line contains one integer n ( 2<=n<=150000 ) — the number of problems.
The second line contains n integers p1,p2,...,pn ( 1<=pi<=108 ) — initial scores.
The third line contains n integers t1,t2,...,tn ( 1<=ti<=108 ) where ti is the number of minutes needed to solve the i -th problem.
输出格式
Print one real value on a single line — the maximum value of c that 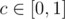 and there is no optimal order with a paradox. Your answer will be considered correct if its absolute or relative error does not exceed 10−6 .
and there is no optimal order with a paradox. Your answer will be considered correct if its absolute or relative error does not exceed 10−6 .
Namely: let's assume that your answer is a , and the answer of the jury is b . The checker program will consider your answer correct if 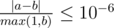 .
.
输入输出样例
输入#1
3 4 3 10 1 1 8
输出#1
0.62500000000
输入#2
4 7 20 15 10 7 20 15 10
输出#2
0.31901840491
输入#3
2 10 20 10 1
输出#3
1.00000000000
说明/提示
In the first sample, there are 3 problems. The first is (4,1) (initial score is 4 and required time is 1 minute), the second problem is (3,1) and the third one is (10,8) . The total time is T=1+1+8=10 .
Let's show that there is a paradox for c=0.7 . Solving problems in order 1 , 2 , 3 turns out to give the best total score, equal to the sum of:
- solved 1 minute after the start:
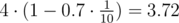
- solved 2 minutes after the start:
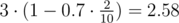
- solved 10 minutes after the start:
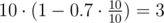
So, this order gives 3.72+2.58+3=9.3 points in total and this is the only optimal order (you can calculate total scores for other 5 possible orders too see that they are lower). You should check points for problems 1 and 3 to see a paradox. There is 4<10 but 3.72>3 . It turns out that there is no paradox for c=0.625 but there is a paradox for any bigger c .
In the second sample, all 24 orders are optimal.
In the third sample, even for c=1 there is no paradox.