CF641F.Little Artem and 2-SAT

Little Artem is a very smart programmer. He knows many different difficult algorithms. Recently he has mastered in 2-SAT one.

In computer science, 2-satisfiability (abbreviated as 2-SAT) is the special case of the problem of determining whether a conjunction (logical AND) of disjunctions (logical OR) have a solution, in which all disjunctions consist of no more than two arguments (variables). For the purpose of this problem we consider only 2-SAT formulas where each disjunction consists of exactly two arguments.

Consider the following 2-SAT problem as an example: 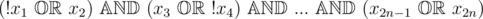. Note that there might be negations in 2-SAT formula (like for $x_{1}$ and for $x_{4}$ ).

Artem now tries to solve as many problems with 2-SAT as possible. He found a very interesting one, which he can not solve yet. Of course, he asks you to help him.

The problem is: given two 2-SAT formulas $f$ and $g$ , determine whether their sets of possible solutions are the same. Otherwise, find any variables assignment $x$ such that $f(x)≠g(x)$ .

The first line of the input contains three integers $n$ , $m_{1}$ and $m_{2}$ ( $1<=n<=1000$ , $1<=m_{1},m_{2}<=n^{2}$ ) — the number of variables, the number of disjunctions in the first formula and the number of disjunctions in the second formula, respectively.

Next $m_{1}$ lines contains the description of 2-SAT formula $f$ . The description consists of exactly $m_{1}$ pairs of integers $x_{i}$ ( $-n<=x_{i}<=n,x_{i}≠0$ ) each on separate line, where x_{i}>0 corresponds to the variable without negation, while x_{i}<0 corresponds to the variable with negation. Each pair gives a single disjunction. Next $m_{2}$ lines contains formula $g$ in the similar format.

If both formulas share the same set of solutions, output a single word "SIMILAR" (without quotes). Otherwise output exactly $n$ integers $x_{i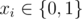}$ () — any set of values $x$ such that $f(x)≠g(x)$ .

First sample has two equal formulas, so they are similar by definition.

In second sample if we compute first function with $x_{1}=0$ and $x_{2}=0$ we get the result $0$ , because 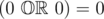. But the second formula is $1$ , because .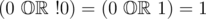