CF618G.Combining Slimes
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Your friend recently gave you some slimes for your birthday. You have a very large amount of slimes with value 1 and 2 , and you decide to invent a game using these slimes.
You initialize a row with n empty spaces. You also choose a number p to be used in the game. Then, you will perform the following steps while the last space is empty.
- With probability
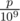 , you will choose a slime with value 1 , and with probability
, you will choose a slime with value 1 , and with probability 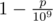 , you will choose a slime with value 2 . You place the chosen slime on the last space of the board.
, you will choose a slime with value 2 . You place the chosen slime on the last space of the board. - You will push the slime to the left as far as possible. If it encounters another slime, and they have the same value v , you will merge the slimes together to create a single slime with value v+1 . This continues on until the slime reaches the end of the board, or encounters a slime with a different value than itself.
You have played the game a few times, but have gotten bored of it. You are now wondering, what is the expected sum of all values of the slimes on the board after you finish the game.
输入格式
The first line of the input will contain two integers n,p ( 1<=n<=10^{9},1<=p<10^{9} ).
输出格式
Print the expected sum of all slimes on the board after the game finishes. Your answer will be considered correct if its absolute or relative error does not exceed 10−4 .
Namely, let's assume that your answer is a and the answer of the jury is b . The checker program will consider your answer correct, if 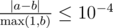 .
.
输入输出样例
输入#1
2 500000000
输出#1
3.562500000000000
输入#2
10 1
输出#2
64.999983360007620
输入#3
100 123456789
输出#3
269.825611298854770
说明/提示
In the first sample, we have a board with two squares, and there is a 0.5 probability of a 1 appearing and a 0.5 probability of a 2 appearing.
Our final board states can be 1 2 with probability 0.25 , 2 1 with probability 0.375 , 3 2 with probability 0.1875 , 3 1 with probability 0.1875 . The expected value is thus (1+2)⋅0.25+(2+1)⋅0.375+(3+2)⋅0.1875+(3+1)⋅0.1875=3.5625 .