CF626D.Jerry's Protest
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Andrew and Jerry are playing a game with Harry as the scorekeeper. The game consists of three rounds. In each round, Andrew and Jerry draw randomly without replacement from a jar containing n balls, each labeled with a distinct positive integer. Without looking, they hand their balls to Harry, who awards the point to the player with the larger number and returns the balls to the jar. The winner of the game is the one who wins at least two of the three rounds.
Andrew wins rounds 1 and 2 while Jerry wins round 3, so Andrew wins the game. However, Jerry is unhappy with this system, claiming that he will often lose the match despite having the higher overall total. What is the probability that the sum of the three balls Jerry drew is strictly higher than the sum of the three balls Andrew drew?
输入格式
The first line of input contains a single integer n ( 2<=n<=2000 ) — the number of balls in the jar.
The second line contains n integers ai ( 1<=ai<=5000 ) — the number written on the i th ball. It is guaranteed that no two balls have the same number.
输出格式
Print a single real value — the probability that Jerry has a higher total, given that Andrew wins the first two rounds and Jerry wins the third. Your answer will be considered correct if its absolute or relative error does not exceed 10−6 .
Namely: let's assume that your answer is a , and the answer of the jury is b . The checker program will consider your answer correct, if 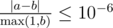 .
.
输入输出样例
输入#1
2 1 2
输出#1
0.0000000000
输入#2
3 1 2 10
输出#2
0.0740740741
说明/提示
In the first case, there are only two balls. In the first two rounds, Andrew must have drawn the 2 and Jerry must have drawn the 1 , and vice versa in the final round. Thus, Andrew's sum is 5 and Jerry's sum is 4 , so Jerry never has a higher total.
In the second case, each game could've had three outcomes — 10−2 , 10−1 , or 2−1 . Jerry has a higher total if and only if Andrew won 2−1 in both of the first two rounds, and Jerry drew the 10 in the last round. This has probability 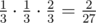 .
.