CF594D.REQ

Today on a math lesson the teacher told Vovochka that the Euler function of a positive integer $φ(n)$ is an arithmetic function that counts the positive integers less than or equal to n that are relatively prime to n. The number $1$ is coprime to all the positive integers and $φ(1)=1$ .

Now the teacher gave Vovochka an array of $n$ positive integers $a_{1},a_{2},...,a_{n}$ and a task to process $q$ queries $l_{i}$ $r_{i}$ — to calculate and print 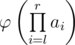modulo $10^{9}+7$ . As it is too hard for a second grade school student, you've decided to help Vovochka.

The first line of the input contains number $n$ ( $1<=n<=200000$ ) — the length of the array given to Vovochka. The second line contains $n$ integers $a_{1},a_{2},...,a_{n}$ ( $1<=a_{i}<=10^{6}$ ).

The third line contains integer $q$ ( $1<=q<=200000$ ) — the number of queries. Next $q$ lines contain the queries, one per line. Each query is defined by the boundaries of the segment $l_{i}$ and $r_{i}$ ( $1<=l_{i}<=r_{i}<=n$ ).

Print $q$ numbers — the value of the Euler function for each query, calculated modulo $10^{9}+7$ .

In the second sample the values are calculated like that:

• $φ(13·52·6)=φ(4056)=1248$
• $φ(52·6·10·1)=φ(3120)=768$
• $φ(24·63·13·52·6·10·1)=φ(61326720)=12939264$
• $φ(63·13·52)=φ(42588)=11232$
• $φ(13·52·6·10)=φ(40560)=9984$
• $φ(63·13·52·6·10)=φ(2555280)=539136$