CF603B.Moodular Arithmetic
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
As behooves any intelligent schoolboy, Kevin Sun is studying psycowlogy, cowculus, and cryptcowgraphy at the Bovinia State University (BGU) under Farmer Ivan. During his Mathematics of Olympiads (MoO) class, Kevin was confronted with a weird functional equation and needs your help. For two fixed integers k and p , where p is an odd prime number, the functional equation states that
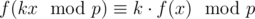 for some function
for some function 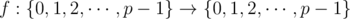 . (This equation should hold for any integer x in the range 0 to p−1 , inclusive.)
. (This equation should hold for any integer x in the range 0 to p−1 , inclusive.)
It turns out that f can actually be many different functions. Instead of finding a solution, Kevin wants you to count the number of distinct functions f that satisfy this equation. Since the answer may be very large, you should print your result modulo 109+7 .
输入格式
The input consists of two space-separated integers p and k ( 3<=p<=1000000 , 0<=k<=p−1 ) on a single line. It is guaranteed that p is an odd prime number.
输出格式
Print a single integer, the number of distinct functions f modulo 109+7 .
输入输出样例
输入#1
3 2
输出#1
3
输入#2
5 4
输出#2
25
说明/提示
In the first sample, p=3 and k=2 . The following functions work:
- f(0)=0 , f(1)=1 , f(2)=2 .
- f(0)=0 , f(1)=2 , f(2)=1 .
- f(0)=f(1)=f(2)=0 .