CF610C.Harmony Analysis

The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find $4$ vectors in $4$ -dimensional space, such that every coordinate of every vector is $1$ or $-1$ and any two vectors are orthogonal. Just as a reminder, two vectors in $n$ -dimensional space are considered to be orthogonal if and only if their scalar product is equal to zero, that is:

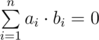.Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for $2^{k}$ vectors in $2^{k}$ -dimensinoal space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?

The only line of the input contains a single integer $k$ ( $0<=k<=9$ ).

Print $2^{k}$ lines consisting of $2^{k}$ characters each. The $j$ -th character of the $i$ -th line must be equal to ' $*$ ' if the $j$ -th coordinate of the $i$ -th vector is equal to $-1$ , and must be equal to ' $+$ ' if it's equal to $+1$ . It's guaranteed that the answer always exists.

If there are many correct answers, print any.

Consider all scalar products in example:

• Vectors $1$ and $2$ : $(+1)·(+1)+(+1)·(-1)+(-1)·(+1)+(-1)·(-1)=0$
• Vectors $1$ and $3$ : $(+1)·(+1)+(+1)·(+1)+(-1)·(+1)+(-1)·(+1)=0$
• Vectors $1$ and $4$ : $(+1)·(+1)+(+1)·(-1)+(-1)·(-1)+(-1)·(+1)=0$
• Vectors $2$ and $3$ : $(+1)·(+1)+(-1)·(+1)+(+1)·(+1)+(-1)·(+1)=0$
• Vectors $2$ and $4$ : $(+1)·(+1)+(-1)·(-1)+(+1)·(-1)+(-1)·(+1)=0$
• Vectors $3$ and $4$ : $(+1)·(+1)+(+1)·(-1)+(+1)·(-1)+(+1)·(+1)=0$