CF611C.New Year and Domino
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
They say "years are like dominoes, tumbling one after the other". But would a year fit into a grid? I don't think so.
Limak is a little polar bear who loves to play. He has recently got a rectangular grid with h rows and w columns. Each cell is a square, either empty (denoted by '.') or forbidden (denoted by '#'). Rows are numbered 1 through h from top to bottom. Columns are numbered 1 through w from left to right.
Also, Limak has a single domino. He wants to put it somewhere in a grid. A domino will occupy exactly two adjacent cells, located either in one row or in one column. Both adjacent cells must be empty and must be inside a grid.
Limak needs more fun and thus he is going to consider some queries. In each query he chooses some rectangle and wonders, how many way are there to put a single domino inside of the chosen rectangle?
输入格式
The first line of the input contains two integers h and w ( 1<=h,w<=500 ) – the number of rows and the number of columns, respectively.
The next h lines describe a grid. Each line contains a string of the length w . Each character is either '.' or '#' — denoting an empty or forbidden cell, respectively.
The next line contains a single integer q ( 1<=q<=100000 ) — the number of queries.
Each of the next q lines contains four integers r1i , c1i , r2i , c2i ( 1<=r1i<=r2i<=h,1<=c1i<=c2i<=w ) — the i -th query. Numbers r1i and c1i denote the row and the column (respectively) of the upper left cell of the rectangle. Numbers r2i and c2i denote the row and the column (respectively) of the bottom right cell of the rectangle.
输出格式
Print q integers, i -th should be equal to the number of ways to put a single domino inside the i -th rectangle.
输入输出样例
输入#1
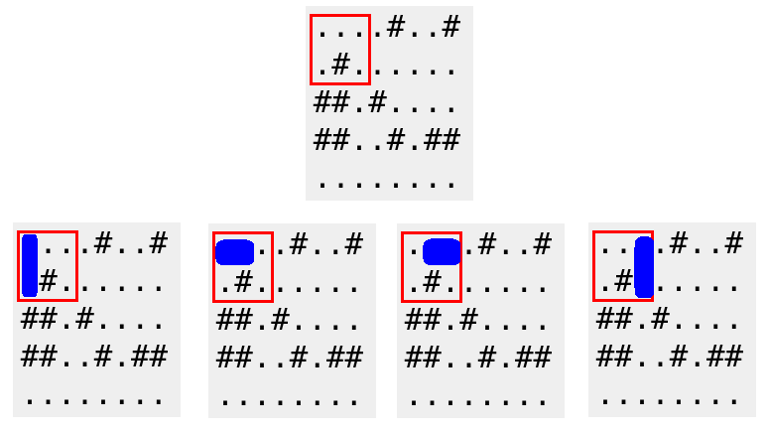
5 8 ....#..# .#...... ##.#.... ##..#.## ........ 4 1 1 2 3 4 1 4 1 1 2 4 5 2 5 5 8
输出#1
4 0 10 15
输入#2
7 39 ....................................... .###..###..#..###.....###..###..#..###. ...#..#.#..#..#.........#..#.#..#..#... .###..#.#..#..###.....###..#.#..#..###. .#....#.#..#....#.....#....#.#..#..#.#. .###..###..#..###.....###..###..#..###. ....................................... 6 1 1 3 20 2 10 6 30 2 10 7 30 2 2 7 7 1 7 7 7 1 8 7 8
输出#2
53 89 120 23 0 2
说明/提示
A red frame below corresponds to the first query of the first sample. A domino can be placed in 4 possible ways.