CF576C.Points on Plane

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

On a plane are $n$ points ( $x_{i}$ , $y_{i}$ ) with integer coordinates between $0$ and $10^{6}$ . The distance between the two points with numbers $a$ and $b$ is said to be the following value: 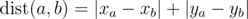(the distance calculated by such formula is called Manhattan distance).

We call a hamiltonian path to be some permutation $p_{i}$ of numbers from $1$ to $n$ . We say that the length of this path is value .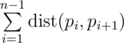

Find some hamiltonian path with a length of no more than $25×10^{8}$ . Note that you do not have to minimize the path length.

输入格式

The first line contains integer $n$ ( $1<=n<=10^{6}$ ).

The $i+1$ -th line contains the coordinates of the $i$ -th point: $x_{i}$ and $y_{i}$ ( $0<=x_{i},y_{i}<=10^{6}$ ).

It is guaranteed that no two points coincide.

输出格式

Print the permutation of numbers $p_{i}$ from $1$ to $n$ — the sought Hamiltonian path. The permutation must meet the inequality .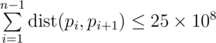

If there are multiple possible answers, print any of them.

It is guaranteed that the answer exists.

输入输出样例

输入#1
```
5
0 7
8 10
3 4
5 0
9 12
```
输出#1
```
4 3 1 2 5 
```

说明/提示

In the sample test the total distance is:

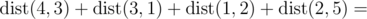
$(|5-3|+|0-4|)+(|3-0|+|4-7|)+(|0-8|+|7-10|)+(|8-9|+|10-12|)=2+4+3+3+8+3+1+2=26$

首页