CF542C.Idempotent functions

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Some time ago Leonid have known about idempotent functions. Idempotent function defined on a set ${1,2,...,n}$ is such function 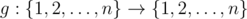, that for any 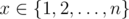the formula $g(g(x))=g(x)$ holds.

Let's denote as $f^{(k)}(x)$ the function $f$ applied $k$ times to the value $x$ . More formally, $f^{(1)}(x)=f(x)$ , $f^{(k)}(x)=f(f^{(k-1)}(x))$ for each k>1 .

You are given some function 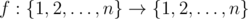. Your task is to find minimum positive integer $k$ such that function $f^{(k)}(x)$ is idempotent.

输入格式

In the first line of the input there is a single integer $n$ ( $1<=n<=200$ ) — the size of function $f$ domain.

In the second line follow $f(1),f(2),...,f(n)$ ( $1<=f(i)<=n$ for each $1<=i<=n$ ), the values of a function.

输出格式

Output minimum $k$ such that function $f^{(k)}(x)$ is idempotent.

输入输出样例

输入#1
```
4
1 2 2 4
```
输出#1
```
1
```
输入#2
```
3
2 3 3
```
输出#2
```
2
```
输入#3
```
3
2 3 1
```
输出#3
```
3
```

说明/提示

In the first sample test function $f(x)=f^{(1)}(x)$ is already idempotent since $f(f(1))=f(1)=1$ , $f(f(2))=f(2)=2$ , $f(f(3))=f(3)=2$ , $f(f(4))=f(4)=4$ .

In the second sample test:

function $f(x)=f^{(1)}(x)$ isn't idempotent because $f(f(1))=3$ but $f(1)=2$ ;
function $f(x)=f^{(2)}(x)$ is idempotent since for any $x$ it is true that $f^{(2)}(x)=3$ , so it is also true that $f^{(2)}(f^{(2)}(x))=3$ .

In the third sample test:

function $f(x)=f^{(1)}(x)$ isn't idempotent because $f(f(1))=3$ but $f(1)=2$ ;
function $f(f(x))=f^{(2)}(x)$ isn't idempotent because $f^{(2)}(f^{(2)}(1))=2$ but $f^{(2)}(1)=3$ ;
function $f(f(f(x)))=f^{(3)}(x)$ is idempotent since it is identity function: $f^{(3)}(x)=x$ for any 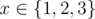meaning that the formula $f^{(3)}(f^{(3)}(x))=f^{(3)}(x)$ also holds.

首页