CF509D.Restoring Numbers

Vasya had two arrays consisting of non-negative integers: $a$ of size $n$ and $b$ of size $m$ . Vasya chose a positive integer $k$ and created an $n×m$ matrix $v$ using the following formula:

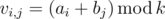Vasya wrote down matrix $v$ on a piece of paper and put it in the table.

A year later Vasya was cleaning his table when he found a piece of paper containing an $n×m$ matrix $w$ . He remembered making a matrix one day by the rules given above but he was not sure if he had found the paper with the matrix $v$ from those days. Your task is to find out if the matrix $w$ that you've found could have been obtained by following these rules and if it could, then for what numbers $k,a_{1},a_{2},...,a_{n},b_{1},b_{2},...,b_{m}$ it is possible.

The first line contains integers $n$ and $m$ ( $1<=n,m<=100$ ), separated by a space — the number of rows and columns in the found matrix, respectively.

The $i$ -th of the following lines contains numbers $w_{i,1},w_{i,2},...,w_{i,m}$ ( $0<=w_{i,j}<=10^{9}$ ), separated by spaces — the elements of the $i$ -th row of matrix $w$ .

If the matrix $w$ could not have been obtained in the manner described above, print "NO" (without quotes) in the single line of output.

Otherwise, print four lines.

In the first line print "YES" (without quotes).

In the second line print an integer $k$ ( $1<=k<=10^{18}$ ). Note that each element of table $w$ should be in range between $0$ and $k-1$ inclusively.

In the third line print $n$ integers $a_{1},a_{2},...,a_{n}$ ( $0<=a_{i}<=10^{18}$ ), separated by spaces.

In the fourth line print $m$ integers $b_{1},b_{2},...,b_{m}$ ( $0<=b_{i}<=10^{18}$ ), separated by spaces.

By 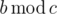we denote the remainder of integer division of $b$ by $c$ .

It is guaranteed that if there exists some set of numbers $k,a_{1},...,a_{n},b_{1},...,b_{m}$ , that you could use to make matrix $w$ , then there also exists a set of numbers that meets the limits $1<=k<=10^{18}$ , $1<=a_{i}<=10^{18}$ , $1<=b_{i}<=10^{18}$ in the output format. In other words, these upper bounds are introduced only for checking convenience purposes.