CF510E.Fox And Dinner

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Fox Ciel is participating in a party in Prime Kingdom. There are $n$ foxes there (include Fox Ciel). The i-th fox is $a_{i}$ years old.

They will have dinner around some round tables. You want to distribute foxes such that:

Each fox is sitting at some table.
Each table has at least 3 foxes sitting around it.
The sum of ages of any two adjacent foxes around each table should be a prime number.

If $k$ foxes $f_{1}$ , $f_{2}$ , ..., $f_{k}$ are sitting around table in clockwise order, then for $1<=i<=k-1$ : $f_{i}$ and $f_{i+1}$ are adjacent, and $f_{1}$ and $f_{k}$ are also adjacent.

If it is possible to distribute the foxes in the desired manner, find out a way to do that.

输入格式

The first line contains single integer $n$ ( $3<=n<=200$ ): the number of foxes in this party.

The second line contains $n$ integers $a_{i}$ ( $2<=a_{i}<=10^{4}$ ).

输出格式

If it is impossible to do this, output "Impossible".

Otherwise, in the first line output an integer $m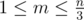$ (): the number of tables.

Then output $m$ lines, each line should start with an integer $k$ -=– the number of foxes around that table, and then $k$ numbers — indices of fox sitting around that table in clockwise order.

If there are several possible arrangements, output any of them.

输入输出样例

输入#1
```
4
3 4 8 9
```
输出#1
```
1
4 1 2 4 3
```
输入#2
```
5
2 2 2 2 2
```
输出#2
```
Impossible
```

输入#3

12
2 3 4 5 6 7 8 9 10 11 12 13

输出#3

1
12 1 2 3 6 5 12 9 8 7 10 11 4

输入#4

24
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

输出#4

3
6 1 2 3 6 5 4
10 7 8 9 12 15 14 13 16 11 10
8 17 18 23 22 19 20 21 24

说明/提示

In example 1, they can sit around one table, their ages are: 3-8-9-4, adjacent sums are: 11, 17, 13 and 7, all those integers are primes.

In example 2, it is not possible: the sum of 2+2 = 4 is not a prime number.

首页