CF513G1.Inversions problem

You are given a permutation of $n$ numbers $p_{1},p_{2},...,p_{n}$ . We perform $k$ operations of the following type: choose uniformly at random two indices $l$ and $r$ ( $l<=r$ ) and reverse the order of the elements $p_{l},p_{l+1},...,p_{r}$ . Your task is to find the expected value of the number of inversions in the resulting permutation.

The first line of input contains two integers $n$ and $k$ ( $1<=n<=100$ , $1<=k<=10^{9}$ ). The next line contains $n$ integers $p_{1},p_{2},...,p_{n}$ — the given permutation. All $p_{i}$ are different and in range from 1 to $n$ .

The problem consists of three subproblems. The subproblems have different constraints on the input. You will get some score for the correct submission of the subproblem. The description of the subproblems follows.

• In subproblem G1 ( $3$ points), the constraints $1<=n<=6$ , $1<=k<=4$ will hold.
• In subproblem G2 ( $5$ points), the constraints $1<=n<=30$ , $1<=k<=200$ will hold.
• In subproblem G3 ( $16$ points), the constraints $1<=n<=100$ , $1<=k<=10^{9}$ will hold.

Output the answer with absolute or relative error no more than $1e-9$ .

Consider the first sample test. We will randomly pick an interval of the permutation $(1,2,3)$ (which has no inversions) and reverse the order of its elements. With probability , the interval will consist of a single element and the permutation will not be altered. With probability we will inverse the first two elements' order and obtain the permutation $(2,1,3)$ which has one inversion. With the same probability we might pick the interval consisting of the last two elements which will lead to the permutation $(1,3,2)$ with one inversion. Finally, with probability the randomly picked interval will contain all elements, leading to the permutation $(3,2,1)$ with 3 inversions. Hence, the expected number of inversions is equal to 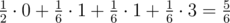.