CF166C.Median

A median in an array with the length of $n$ is an element which occupies position number 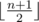after we sort the elements in the non-decreasing order (the array elements are numbered starting with $1$ ). A median of an array $(2,6,1,2,3)$ is the number $2$ , and a median of array $(0,96,17,23)$ — the number $17$ .

We define an expression 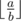as the integer part of dividing number $a$ by number $b$ .

One day Vasya showed Petya an array consisting of $n$ integers and suggested finding the array's median. Petya didn't even look at the array and said that it equals $x$ . Petya is a very honest boy, so he decided to add several numbers to the given array so that the median of the resulting array would be equal to $x$ .

Petya can add any integers from $1$ to $10^{5}$ to the array, including the same numbers. Of course, he can add nothing to the array. If a number is added multiple times, then we should consider it the number of times it occurs. It is not allowed to delete of change initial numbers of the array.

While Petya is busy distracting Vasya, your task is to find the minimum number of elements he will need.

The first input line contains two space-separated integers $n$ and $x$ ( $1<=n<=500$ , $1<=x<=10^{5}$ ) — the initial array's length and the required median's value. The second line contains $n$ space-separated numbers — the initial array. The elements of the array are integers from $1$ to $10^{5}$ . The array elements are not necessarily different.

Print the only integer — the minimum number of elements Petya needs to add to the array so that its median equals $x$ .

In the first sample we can add number $9$ to array $(10,20,30)$ . The resulting array $(9,10,20,30)$ will have a median in position 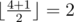, that is, $10$ .

In the second sample you should add numbers $4$ , $5$ , $5$ , $5$ . The resulting array has median equal to $4$ .