A101182.[Cnoi2020] 线形生物

题目背景

为了能够在冥界过上这种愉快的生活而不是被判入地狱，人类们摒弃了自行结束生命的做法，拼尽全力地生活着。如此看来，人类似乎也显得有些积极与可爱了呢。 （射命丸 文）

线形生物沿着一维的阶梯向着冥界单向地前行着。

照这样的话，它只需要一级一级地，走 $n$ 步就能够到达白玉楼。

但 Cirno 觉得这样太单调了，于是，一维的壁垒被打破，链状的道路生出了花椰菜状的枝桠。

题目描述

线形生物要从 $1$ 号台阶走到 $n+1$ 号台阶。

最开始，$1,2,3,\ldots,n$ 号台阶都有一条连向下一台阶的有向边 $i\rightarrow i+1$。

之后 Cirno 加入了 $m$ 条返祖边 $u_i \rightarrow v_i (u_i \ge v_i)$，它们构成了一个返祖图。

线形生物每步会 等概率地 选取当前台阶的一条出边并走向对应的台阶。

当走到 $n+1$ 号台阶时，线形生物就会停止行走。

同时，Cirno 会统计线性生物总共走的步数，记作 $\delta$。

Cirno 想知道 $E(\delta)$（即 $\delta$ 的数学期望）对 $998244353$ 取模后的结果。

第一行三个整数 $id$，$n$，$m$。

以下 $m$ 行，每行两个整数 $u_i$，$v_i$。

$id$ 表示 subtask 编号，其它字母含义同上文。

一行，一个整数 $E(\delta)$，字母含义同上文。

后置数学知识

• 可能用到的幂级数求和 : 若 $x>1$，则有 $\sum\limits_{i=1}^{\infty}\big(\frac{1}{x}\big)^i=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x^3}+\cdots=\frac{1}{x-1}$。
• 数学期望 : 随机试验中每次可能结果的概率乘以其结果的总和，反映随机变量平均取值的大小。
• 离散期望公式 : $E(x)=\sum\limits_{k=1}^{\infty}x_kp_k$。

数据范围与约定

对于 $100\%$ 的数据，保证：$id \in \{1,2,3,4,5\}$，$0 < n,m \le 10^6$，$1 \le v_i \le u_i \le n$。

子任务「本题采用捆绑测试」

• Subtask1（$10\%$）: 返祖图中所有点都有自环且所有边均为自环(未画出)，总图形如 :
  

• Subtask2（$10\%$）: 返祖图中所有点均向且仅向自己的前驱连边，特别地，$1$ 号节点的前驱是 $1$ 号节点，总图形如 :
  

• Subtask3（$10\%$）: 返祖图中所有点均向且仅向 $1$ 号节点连边，总图形如 :
  

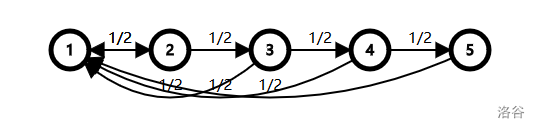
• Subtask4（$10\%$）: $n \le 100$，$m \le 1000$。

• Subtask5（$60\%$）: 无特殊限制。