A101176.Control of Randomness

定一棵树，树上有 $ n $ 个顶点。

我们在某个顶点 $ v \ne 1 $ 放置一个机器人，最初拥有 $ p $ 枚硬币。以下是机器人的移动规则：

• 当 $ i $ 为奇数时，机器人会向顶点 $ 1 $ 的方向移动到相邻的节点。
• 当 $ i $ 为偶数时，如果你愿意支付一枚硬币并且还有剩余的硬币，则机器人会向顶点 $ 1 $ 的方向移动到相邻的节点；否则，机器人将随机选择一个相邻的节点移动。

当机器人到达顶点 $ 1 $ 时，过程终止。记 $ f(v, p) $ 为通过最佳策略使用硬币时，使得上述过程的期望步数最小值。

你的任务是解决 $ q $ 个查询。每个查询包含一对 $(v_i, p_i)$，你需要计算 $ f(v_i, p_i) $ 模 $ 998,244,353 $ 的值。

具体来说，令 $ M = 998,244,353 $。结果可以表示为一个不可约分数 $ \frac{p}{q} $，其中 $ p $ 和 $ q $ 是整数且 $ q \not\equiv 0 \pmod{M} $。你需要输出 $ p \cdot q^{-1} \bmod M $。换句话说，输出满足 $ 0 \le x < M $ 且 $ x \cdot q \equiv p \pmod{M} $ 的整数 $ x $。

输入包含多个测试用例。第一行为测试用例的数量 $ t $ （$ 1 \le t \le 10^3 $）。

对于每个测试用例，第一行包含两个整数 $ n $ 和 $ q $（$ 2 \le n \le 2000 $，$ 1 \le q \le 2000 $），分别表示树的顶点数和查询数量。

接下来的 $ n - 1 $ 行每行描述一条树的边，包含两个整数 $ u_i $ 和 $ v_i $ （$ 1 \le u_i, v_i \le n $，$ u_i \neq v_i $），表示节点 $ u_i $ 和 $ v_i $ 之间有一条边。

接下来的 $ q $ 行中每行包含两个整数 $ v_i $ 和 $ p_i $（$ 2 \le v_i \le n $，$ 0 \le p_i \le n $），表示每个查询的节点和初始硬币数。

保证输入的边构成一棵树，并且所有测试用例的 $ n $ 之和不超过 $ 2000 $，$ q $ 之和不超过 $ 2000 $。

对于每个测试用例，输出 $ q $ 个整数，表示每个查询 $ f(v_i, p_i) $ 模 $ 998,244,353 $ 的结果。

形式上，令 $ M = 998,244,353 $。可以证明答案可以表示为不可约分数 $ \frac{p}{q} $，其中 $ p $ 和 $ q $ 是整数且 $ q \not\equiv 0 \pmod{M} $。输出满足 $ 0 \le x < M $ 且 $ x \cdot q \equiv p \pmod{M} $ 的整数 $ x $。

在第一个测试用例中，树的结构如下：

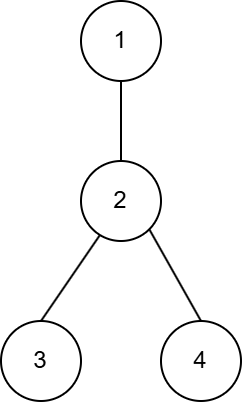
第一个查询中，期望值为 $ 1 $，因为机器人从顶点 $ 2 $ 出发，一步就到达了顶点 $ 1 $，过程结束。

第二个查询中的期望步数计算如下（$ x $ 为步数）：

• $ P(x < 2) = 0 $，因为距离顶点 $ 1 $ 是 $ 2 $，机器人无法在更少的步数内到达。
• $ P(x = 2) = \frac{1}{3} $，因为只有一种步骤序列使 $ x = 2 $。即 $ 3 \rightarrow_{1} 2 \rightarrow_{0.33} 1 $，概率为 $ 1 \cdot \frac{1}{3} $。
• $ P(x \bmod 2 = 1) = 0 $，因为机器人只能通过偶数步数到达顶点 $ 1 $。
• $ P(x = 4) = \frac{2}{9} $：可能路径为 $ 3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1 $。
• $ P(x = 6) = \frac{4}{27} $：可能路径为 $ 3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1 $。
• 一般情况下，$ P(x = i \cdot 2) = \frac{2^{i - 1}}{3^i} $。

因此，$ f(v, p) = \sum_{i=1}^{\infty}{i \cdot 2 \cdot \frac{2^{i - 1}}{3^i}} = 6 $。

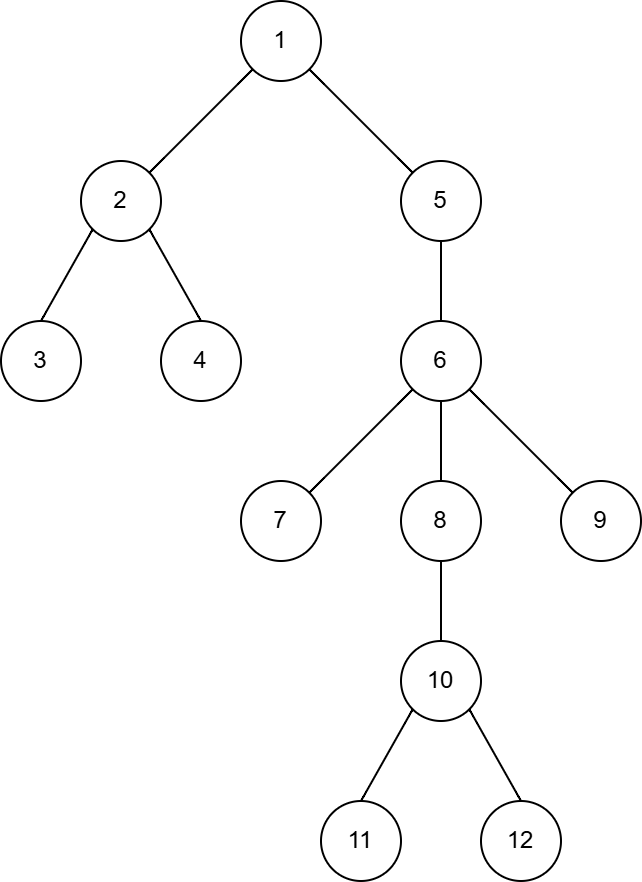
第二个测试用例中，树的结构如下：